SMO（Sequential minimal optimization）

引子

前面章节中，我们使用了核函数的软间隔支持向量机的优化模型为：

式 (1) 需要满足的 KKT 条件为：

在 SMO（序列最小化）方法出现之前，人们依赖于二次规划求解工具来解决上述的优化问题，训练 SVM。这些工具需要具有强大计算能力的计算机进行支撑，实现也比较复杂。1998 年，微软研究院的 John Platt 提出了 SMO 算法将优化问题分解为容易求解的若干小的优化问题，来训练 SVM。简言之，SMO 仅关注 对 和 偏置 的求解更新，进而求解出权值向量 ，得到决策边界（分割超平面），从而大大减少了运算复杂度。

算法介绍

SMO 会选择一对 及 ，并固定住其他参数，即将其他参数认为是常数，则式 （1）中的约束条件就可写为：

其中：

那么，式 (1) 的优化问题可以推导：

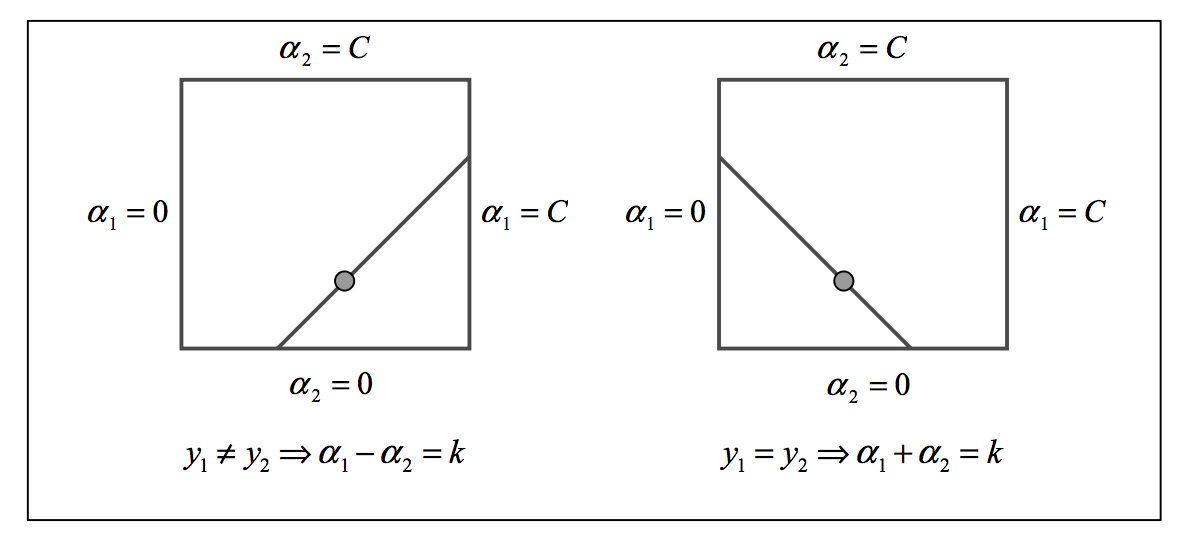
  • 由 知， 及 的取值需要落在正方形中。
  • 由 知， 及 的取值需要落在正方形中取值还需要落到图示的斜线段上。

假设我们放缩了 的取值：

我们可以确定出 的上下界为：

  • 时：

  • 时：

我们将优化函数定义为：

由于 与 有线性关系，所以式 (9) 可以消去 ，进而令 对 求二阶导，并令二阶导为 0 可得（中间过程省略）：

其中：

令：

式 (10) 两边除以 就得 的更新式：

但是，更新还要考虑上下界截断：

从而得到 的更新：

令：

则 的更新为：

启发式选择

根据 Osuna 提出的理论，如果两个拉格朗日乘子其中之一违背了 KKT 条件，此时，每一次乘子对的选择，都能使得优化目标函数减小。

  • 若 ，可知样本 不会对模型 产生影响。
  • 若 ，样本 不会是支持向量。
  • 若 ，则 没有落在边界上，当下式满足时， 会违反 KKT 条件：

通常，式 (18) 过于严苛，因此考虑设置一个容忍区间 ，并考虑令:

可以将违反 KKT 条件的表达式写为：

SMO 以编程的眼光，将启发式选择 描述为了两层循环：

  • 外层循环：外层循环中，如果当前没有 对 的变化，意味着所有 都遵从了 KKT 条件，需要在整个样本集进行迭代；否则，只需要选择在处在边界内（即 ）、并且违反了 KKT 条件（即满足了式 (20) ）的 。
  • 内层循环：选出使得 达到最大的 。

算法流程

综上，我们可以概括出 SMO 的算法流程：

  1. 在整个训练集或者非边界样本中选择违反了 KKT 条件的 。
  2. 在剩下的 中，选择 达到最大的 。
  3. 重复以上过程直到达到收敛精度或最大迭代次数。

参考资料

results matching ""

    No results matching ""