程序示例--K-Means
函数定义
# coding: utf-8
# kmeans/kmeans.py
import numpy as np
def loadDataSet(filename):
"""
读取数据集
Args:
filename: 文件名
Returns:
dataMat: 数据样本矩阵
"""
dataMat = []
fr = open(filename)
for line in fr.readlines():
curLine = line.strip().split('\t')
# 通过map函数批量转换
fitLine = map(float, curLine)
dataMat.append(fitLine)
return dataMat
def distEclud(vecA, vecB):
"""
计算两向量的欧氏距离
Args:
vecA: 向量A
vecB: 向量B
Returns:
欧式距离
"""
return np.sqrt(np.sum(np.power(vecA - vecB, 2)))
def randCent(dataSet, k):
"""
随机生成k个聚类中心
Args:
dataSet: 数据集
k: 簇数目
Returns:
centroids: 聚类中心矩阵
"""
_, n = dataSet.shape
centroids = np.mat(np.zeros((k, n)))
for j in range(n):
# 随机聚类中心落在数据集的边界之内
minJ = np.min(dataSet[:, j])
maxJ = np.max(dataSet[:, j])
rangeJ = float(maxJ - minJ)
centroids[:, j] = minJ + rangeJ * np.random.rand(k, 1)
return centroids
def kMeans(dataSet, k, maxIter = 5):
"""
K-Means
Args:
dataSet: 数据集
k: 聚类数
Returns:
centroids: 聚类中心
clusterAssment: 点分配结果
"""
# 随机初始化聚类中心
centroids = randCent(dataSet, k)
m, n = np.shape(dataSet)
# 点分配结果: 第一列指明样本所在的簇,第二列指明该样本到聚类中心的距离
clusterAssment = np.mat(np.zeros((m, 2)))
# 标识聚类中心是否仍在改变
clusterChanged = True
# 直至聚类中心不再变化
iterCount = 0
while clusterChanged and iterCount < maxIter:
iterCount += 1
clusterChanged = False
# 分配样本到簇
for i in range(m):
# 计算第i个样本到各个聚类中心的距离
minIndex = 0
minDist = np.inf
for j in range(k):
dist = distEclud(dataSet[i, :], centroids[j, :])
if(dist < minDist):
minIndex = j
minDist = dist
# 判断cluster是否改变
if(clusterAssment[i, 0] != minIndex):
clusterChanged = True
clusterAssment[i, :] = minIndex, minDist**2
# 刷新聚类中心: 移动聚类中心到所在簇的均值位置
for cent in range(k):
# 通过数组过滤获得簇中的点
ptsInCluster = dataSet[np.nonzero(
clusterAssment[:, 0].A == cent)[0]]
if ptsInCluster.shape[0] > 0:
# 计算均值并移动
centroids[cent, :] = np.mean(ptsInCluster, axis=0)
return centroids, clusterAssment
我分别测试了 以及 时的聚类效果:

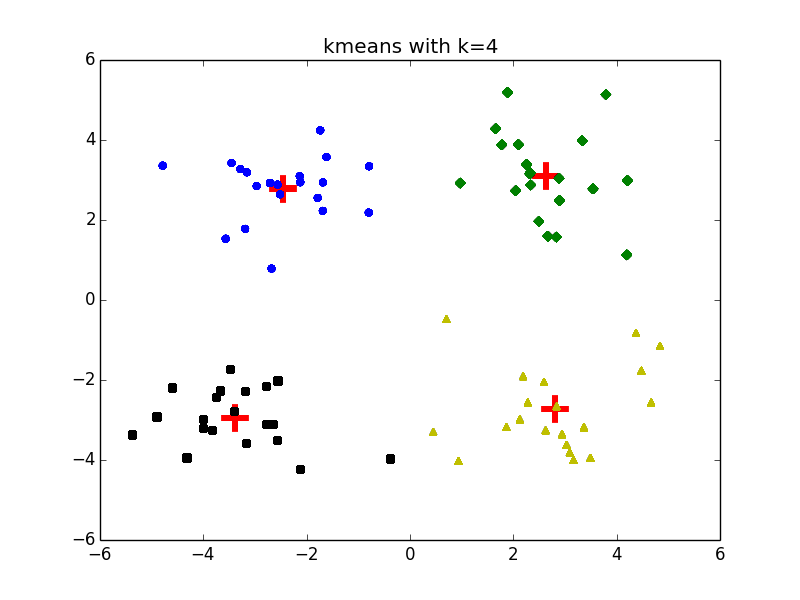
值得一体的是,在 的情况下,还会引起不同的聚类结果:
